1. Contributions
- A flexible and extensible nonlinear method multi-view laplacian least square (MvLLS) is proposed for multi-view human-emotion recognition.
- MvLLS finds a common subspace across all views where the connected samples stay close to each other as well.
- With the global laplacian weighted graph (GLWP), MvLLS records the local structures, introduces the category discriminant information, and protects the local information.
- MvLLS is optimized with interactive method.
- The weighted local preserving embedding (WLPE) is the out-of-sample extension of MvLLS.
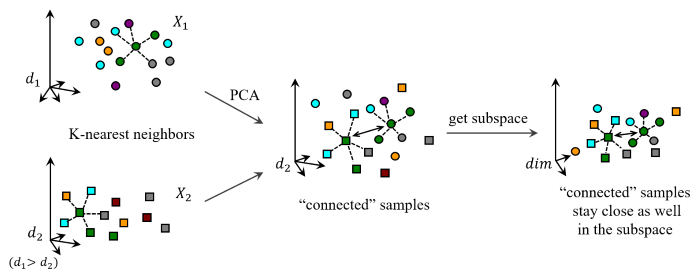
2. Motivations
- There are few nonlinear subspace learning methods proposed.
- The lack of category information or features of some samples could make most of existing methods hard to work.
- In practical applications, I discovered that PLS get much better experimental results compared with CCA.
3. Multi-view laplacian least squares
3.1. Global laplacian weighted graph
With PCA as the preprocessing step, a global laplacian weighted graph (GLWP) \(\mathcal{W}\) is constructed over all views, which is composed by weighted graph of each two views \(W\). Whether two samples in \(W\) are connected or not depends on labels of they and their neighbors. In this way, the category discriminant information and locality is protected.
\[\mathcal{W}= \begin{bmatrix} W^{11} & W^{12} & \cdots & W^{1v} \\ W^{21} & W^{22} & \cdots & W^{2v} \\ \vdots & \vdots & \vdots & \vdots \\ W^{v1} & W^{v2} & \cdots & W^{vv} \\ \end{bmatrix}\]Then the optimization target of MvLLS is formulated as
\[\mathop{\min\limits_{y^1,\cdots,y^v}\sum_{1\le i,j \le v}\xi(i, j)=\sum_{1\le i,j \le v}y^iL^{ij}y^{jT}} \\ =\begin{bmatrix} y^1, y^2, \cdots, y^v \end{bmatrix} \begin{bmatrix} L^{11} & L^{12} & \cdots & L^{1v} \\ L^{21} & L^{22} & \cdots & L^{2v} \\ \vdots & \vdots & \vdots & \vdots \\ L^{v1} & L^{v2} & \cdots & L^{vv} \\ \end{bmatrix} \begin{bmatrix} y^{1T}\\ y^{2T}\\ \vdots\\ y^{vT} \end{bmatrix} \nonumber \\ =\mathcal{Y}\mathcal{L}\mathcal{Y}^T \\ s.t. \ \mathcal{Y}\mathcal{D}\mathcal{Y}^T = 1\]3.2. Laplacian partial least squares
Inspired by PLS, after getting \(\mathcal{Y}\) which is the embeddings of all views on the first dimension of the subspace with \(\mathcal{W}\), we use \(\mathcal{Y}\) as the regressor of \(\mathcal{W}\) to predict it. Then \(\mathcal{W}\) is replaced by the residual matrix. This procedure is repeated for $dim$ times to get the embeddings on each dimension of the target subspace.
\[\mathcal{W} = \ P^T\mathcal{Y} + E \\ \mathcal{W}' = E\]3.3. Weighted local preserving embedding
WLPE looks for an embedding in the subspace that maintains the local neighbors of the high-dimensional space, and the neighbors with higher degrees in GLWM are expected to have greater weights. The embeddings of new samples are regarded as weighted sum of embeddings of its neighbors.
4. Evaluation
We evaluate MvLLS with some state-of-art methods on two datasets and three tasks, experiment results indicate the effectiveness and robustness of MvLLS.